Disclaimer: There are a lot of Sigmas and Pis
Recently, I came across a question that did not seem too difficult at first. But it was this question that led me to think about ways to generalize it which led me to write this article. So, on to the question!
The question was as below:
This question can be solved quite simply using mathematical induction. This can be shown as follows:
So, this proof isn’t particularly difficult. However, as I was looking at this, I recalled the famous formula:
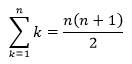
Looking at these two equations, I made a mental connection between both of them. Before I put down my thoughts into an equation, I wanted to test it out with the sum of the products of all integers taken two at a time. When you see that proof, you may be able to make the connection yourself!
So, for this next problem, I phrased the equation as below:
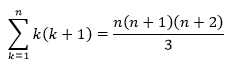
To prove this equation, I used mathematical induction again. This can be shown as:
Now that I was able to show that this equation was also true, I could finally compose all of this work into a single generalized equation:
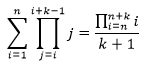
This equation is basically giving a generalized form for the sum of the products of all integers taken k integers at a time. Now, it is time to prove this equation as well! Yet again, we will be using mathematical induction to do this. We will leave k as a variable and work with n. This is shown as below:
Although this working may look complicated, it is essentially the same thing we have done in the 2 proofs before this. And just like that, we have shown what we can compose the sum of the products of all integers taken k integers at a time can be condensed to!
With all this, we can see how we had moved from fairly small problem to a brilliant generalization of it. This is the beauty of math — you can start in one place and end up in a completely different, but equally enchanting, place!